As a tool applied to making an investment decision on whether a project adds value or not, comparing the IRR of a single project with the required rate of return, in isolation from any other projects, is equivalent to the NPV method. However, using IRR to sort projects in order of preference does not result in the same order as using NPV.
This, along with the fact that long projects with fluctuating cash flows may have multiple distinct IRR values, has prompted the use of another metric called modified internal rate of return (MIRR). The internal rate of return is calculated by discounting the present value of future cash flows from the investment with theinternal rate of returnand subtracting the initial investment amount. Given the shortcomings of the method, analysts are using the Modified Internal Rate of Return. It assumes that the positive cash flows are reinvested at the cost of capital and not IRR.
When the calculated IRR is higher than the true reinvestment rate for interim cash flows, the measure will overestimate–sometimes very significantly–the annual equivalent return from the project. The formula assumes that the company has additional projects, with equally attractive prospects, in which to invest the interim cash flows. One advantage of the IRR method is that it is very clear and easy to understand.
This can occur in the unusual case where cash flows change erratically from positive to negative (in large quantities or for sustained time periods) more than once during the life of the investment. The graph in the following example illustrates how multiple IRR roots can occur for investments with these types of cash flows.
It compares expected cash flow of a project to the cost of the capital involved. The internal rate of return (IRR) formula is made out of the interest rates, or discount rates, at which the cashflows of a project (which can be negative or positive) are equal to zero.
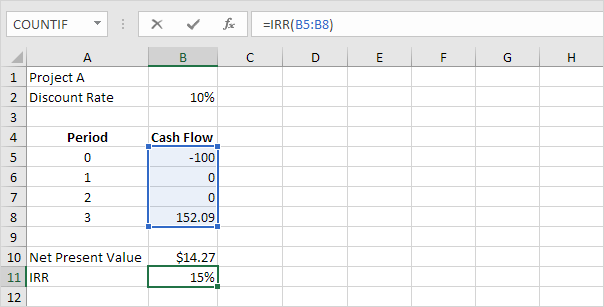
This applies in real life for example when a customer makes a deposit before a specific machine is built. For the computation of the internal rate of return, we use the same formula as NPV. To derive the IRR, an analyst has to rely on trial and error method and cannot use analytical methods. With automation, various software (like Microsoft Excel) is also available to calculate IRR. In Excel, there is a financial function that uses cash flows at regular intervals for calculation.
Rather, when positive cash flows are reinvested, it will be at a rate that more resembles the cost of capital. Miscalculating using IRR in this way may lead to the belief that a project is more profitable than it actually is.
The Internal Rate of Return is a financial indicator, used to determine the attractiveness of an investment or project. It can be defined as the percentage rate earned on each dollar invested, in a defined period of time.

is another widely used capital budgeting technique; essentially, it is the return we will receive over the life of our investment. This is the rate that makes the present value of the cash flows equal to the initial investment. Unfortunately, for some projects there is no easy way to arrive at this rate without using a “guess and check” method; thankfully, computers can do this quite quickly.
Internal Rate of Return – IRR
You also have to be careful about how IRR takes into account the time value of money. IRR assumes future cash flows from a project are reinvested at the IRR, not at the company’s cost of capital, and therefore doesn’t tie as accurately to cost of capital and time value of money as NPV does.
The internal rate of return (IRR) is a metric used in capital budgeting to estimate the profitability of potential investments. The internal rate of return is a discount rate that makes the net present value (NPV) of all cash flows from a particular project equal to zero. The IRR method has several disadvantages compared to the NPV method, though only one disadvantage is mentioned here for purposes of brevity. Further information about potential problems with the IRR method (compared to NPV) may be obtained from most finance textbooks. One major problem with IRR is the possibility of obtaining multiple rates of return (multiple “roots”) when solving for the IRR of an investment.
- The internal rate of return is a discount rate that makes the net present value (NPV) of all cash flows from a particular project equal to zero.
- The internal rate of return (IRR) is a metric used in capital budgeting to estimate the profitability of potential investments.
Computes the Internal Rate of Return (IRR) for a series of equally spaced cash flows («values») along the index «I». The internal rate of return is a widely used criteria for comparing alternative capital investment opportunities. Intuitively, it is the effective compounded rate of return (per time step) on invested capital that is implied by the investment’s future cash flows.
The internal rate of return (IRR) is a tool used by investors and firms for capital budgeting. The IRR is the rate of return (compounded at specific intervals) that a project will earn or lose. This calculation takes into account the expected cash flows adjusted by a discount rate equalizing the NPV to zero. Modified Internal Rate of Return (MIRR) considers cost of capital, and is intended to provide a better indication of a project’s probable return. It applies a discount rate for borrowing cash, and the IRR is calculated for the investment cash flows.
In addition, IRR assumes reinvestment of interim cash flows in projects with equal rates of return (the reinvestment can be the same project or a different project). Therefore, IRR overstates the annual equivalent rate of return for a project whose interim cash flows are reinvested at a rate lower than the calculated IRR. This presents a problem, especially for high IRR projects, since there is frequently not another project available in the interim that can earn the same rate of return as the first project.
Therefore, based on the nature of the formula, the correct answer is option d. However, for capital budgeting, when the objective is to maximize value, finance theory holds that NPV using the firm’s cost of capital is the optimal metric.
IRR has a number of distinct advantages (as does NPV) over both the payback and ROR methods as a decision-making tool for evaluating potential investments. The first advantage is that the IRR calculation takes into account TVM. Therefore, IRR is an objective criterion, rather than a subjective criterion, for making decisions about investment projects. Thirdly, IRR uses actual cash flows rather than accounting incomes like the ROR method. Internal rate of return (IRR) is the interest rate at which the NPV of all the cash flows (both positive and negative) from a project or an investment equals zero.
Assuming all projects require the same amount of up-front investment, the project with the highest IRR would be considered the best and undertaken first. A firm (or individual) should, in theory, undertake all projects or investments available with IRRs that exceed the cost of capital. In other words, an investment is considered acceptable if its internal rate of return is greater than an established minimum acceptable rate of return or cost of capital.
Most analysts and financial managers can understand the opportunity costs of a company. If the IRR exceeds this rate, then the project provides financial accretion.
What Does IRR Tell You?
The internal rate of return (IRR) is one of the most frequently-used metrics for assessing investment opportunities. The IRR is defined as the discount rate for which the NPV of a project is zero. The definition is simple, but the IRR is generally impossible to calculate without a computer.
The IRR is formally defined as the discount rate at which the Net Present Value of the cash flows is equal to zero. For many “normal” capital investments, a large up-front outlay is followed by a stream of revenue into the future eventually totaling an amount greater than the initial investment. For these cash flows, as discount rate increases, NPV decreases, eventually passing from positive to negative NPV. The discount rate where NPV passes through zero, the IRR, is the discount rate at which the project’s value of future earnings is break-even with the initial investment cost.
Limitations of the IRR
The second graph is for comparison purposes and typifies the IRR calculation and graph for most investments. According to Knight, it’s commonly used by financial analysts in conjunction with net present value, or NPV. That’s because the two methods are similar but use different variables.
With NPV you assume a particular discount rate for your company, then calculate the present value of the investment (more here on NPV). But with IRR you calculate the actual return provided by the project’s cash flows, then compare that rate of return with your company’s hurdle rate (how much it mandates that investments return).
Most managers use a spreadsheet, such as Excel, to calculate the IRR for an investment (we discuss this later in the chapter). The goal is simply to find the rate that generates an NPV of zero.
IRR vs. Compound Annual Growth Rate
However, if the rate of an investment is projected to be below the IRR, then the investment would destroy company value. IRR is used in many company financial profiles due its clarity for all parties.