Statistics for the rest of us!
More importantly, the usual use of regression is to take coefficients from the model and then apply them to other data. Since multicollinearity causes imprecise estimates of coefficient values, the resulting out-of-sample predictions will also be imprecise. And if the pattern of multicollinearity in the new data differs from that in the data that was fitted, such extrapolation may introduce large errors in the predictions. A variance inflation factor(VIF) detects multicollinearity in regression analysis.
What is meant by Multicollinearity?
Multicollinearity refers to a situation in which two or more explanatory variables in a multiple regression model are highly linearly related. We have perfect multicollinearity if, for example as in the equation above, the correlation between two independent variables is equal to 1 or1.
Multicollinearity exists whenever an independent variable is highly correlated with one or more of the other independent variables in a multiple regression equation. Multicollinearity is a problem because it undermines the statistical significance of an independent variable. Other things being equal, the larger the standard error of a regression coefficient, the less likely it is that this coefficient will be statistically significant. The coefficients have the expected positive signs, plausible magnitudes, and solid t values.
My concern are the VIF statistics for Avoidance, Distraction and Social Diversion Coping which appear to be very high. Other things being equal, an independent variable that is very highly correlated with one or more other independent variables will have a relatively large standard error. This implies that the partial regression coefficient is unstable and will vary greatly from one sample to the next.
We will also have trouble if some explanatory variables are perfectly correlated with each other. If income and wealth always move in unison, we cannot tell which is responsible for the observed changes in consumption.
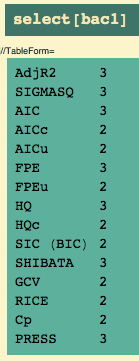
In other words, it results when you have factors that are a bit redundant. So hide the influence that each factor has on response variable. Secondly, I would like to explain how you recognize whether there is multicollinnearity or not. How do we interpret the variance inflation factors for a regression model? A VIF of 1 means that there is no correlation among the jth predictor and the remaining predictor variables, and hence the variance of bj is not inflated at all.
All variables involved in the linear relationship will have a small tolerance. Some suggest that a tolerance value less than 0.1 should be investigated further. If a low tolerance value is accompanied by large standard errors and nonsignificance, multicollinearity may be an issue.
Therefore, In the multiple linear regression analysis, we can easily check multicolinearity by clicking on diagnostic for multicollinearity (or, simply, collinearity) in SPSS of Regression Procedure. But we can solve this problem by using multiple linear regression for the set of independent factors excluding the original response and letting one of the factors as response and check the multicolinearity.
What is Multicollinearity?
Hi Mr. Frost, I am a PhD candidate who is now working on the assumptions for multiple regression analysis. I have purchased your book and have read this article to hopefully help me with testing multicollinearity in the data. I have a problem that I hope you can at least help me shed light on. I chose to conduct a multiple regression analysis for my study in which I have 6 independent variables and one dependent variable. In testing the assumption of multicollinearity, the following are the numbers for Variance and for VIF.
- Recall that we learned previously that the standard errors — and hence the variances — of the estimated coefficients are inflated when multicollinearity exists.
- A variance inflation factor exists for each of the predictors in a multiple regression model.
- As the name suggests, a variance inflation factor (VIF) quantifies how much the variance is inflated.

If these variables were less correlated, the estimates would be more precise. Each coefficient in a multiple regression model tells us the effect on the dependent variable of a change in that explanatory variable, holding the other explanatory variables constant. To obtain reliable estimates, we need a reasonable number of observations and substantial variation in each explanatory variable. We cannot estimate the effect of a change in income on consumption if income never changes.
Why is Multicollinearity a Potential Problem?
Then use the variables with less multicolinearity as the independent factors for the original response. Second option Use Principal Component Analysis / Factor analysis. Third use Scatter plot/pair matrix plot and also correlation matrix of the factors.
Remedies for multicollinearity
Yet, the correlation between the two explanatory variables is 0.98. Income and wealth are strongly positively correlated. As explained earlier, this is a persuasive reason for not omitting either of these important variables. If either variable were omitted, its estimated coefficient would be biased. A helpful refrain is, “When in doubt, don’t leave it out.” Income and wealth were both included because we believe that both should be included in the model.
As the name suggests, a variance inflation factor (VIF) quantifies how much the variance is inflated. Recall that we learned previously that the standard errors — and hence the variances — of the estimated coefficients are inflated when multicollinearity exists. A variance inflation factor exists for each of the predictors in a multiple regression model. So long as the underlying specification is correct, multicollinearity does not actually bias results; it just produces large standard errors in the related independent variables.
In practice, we rarely face perfect multicollinearity in a data set. More commonly, the issue of multicollinearity arises when there is an approximate linear relationship among two or more independent variables. You can assess multicollinearity by examining tolerance and the Variance Inflation Factor (VIF) are two collinearity diagnostic factors that can help you identify multicollinearity. Tolerance is a measure of collinearity reported by most statistical programs such as SPSS; the variable’s tolerance is 1-R2.
Multicollinearity is when there’s correlation between predictors (i.e. independent variables) in a model; it’s presence can adversely affect your regression results. The VIF estimates how much the variance of a regression coefficient is inflated due to multicollinearity in the model. Multicollinearity refers to a situation in which two or more explanatory variables in a multiple regression model are highly linearly related. We have perfect multicollinearity if, for example as in the equation above, the correlation between two independent variables is equal to 1 or1.
The problem of multicollinearity
While you are doing all these techniques you must create dummy variable for categorical independent factors since SPSS do not accept categorical predictors for this procedures. First I’d like to explain what the Multicollinearity mean. Multicollinearity occurs when your model includes multiple factors that are correlated to each other instead just to response variable.